ギリシャ文字は好きですか?
ギリシャ文字って聞くだけでなんだかネガティブなイメージを持ってしまうのは私だけでしょうか…。
数学や物理が思い出さされるから?知ってる文字が少なくて得体が知れないから?
いいイメージが想起されないギリシャ文字ですが、社会人になってからはありがたいことにまったく関わることなく生活ができてました。それなのにです。
オプションやってるとめっちゃギリシャ文字出てくるやないかい!
最初の内は見て見ぬふりをしてましたが、やっぱりよく見かけるってことは重要なんですよね。アレルギー反応がある人も腹をくくってやつらが何を伝えたいのかに少しだけ耳を傾けましょう。
長い間避けていましたが、このギリシャ文字達を確認することでそのオプションが抱えている短期的な値動きの特性を知ることができるのです。
株式では株価の動きがすべてですが、オプションではその他にも価格に影響を与える要素があります。オプション価格の値動きはを感覚で捉えるのは至難の業なので、イメージしていた値動きと実際の値動きが全然違うということが初心者にはよく起こります。知らないうちに過度なリスクにさらされているなんてことも。
ギリシャ文字達はこのイメージしていた値動きと実際の値動きのギャップを埋めてくれる素晴らしいやつなのです。
この記事で紹介するオプショングリークスでまずおさえておくべきは、ΔΓθνの4つだけです。それぞれが何を表しているかを理解するのは難しくありません。
さあ、あなたもギリシャ文字の世界へ。
文字の読み方
ΔΓθνの4文字がぜんぶ読めるって人はこの場でレアキャラ認定したいぐらいのレア具合だと思います。ですので基本中の基本としてまずは読み方から。
- Δ:デルタ
- Γ:ガンマ
- ν:ベガ
- θ:セータ
実際出てくるときは文字ではなくデルタみたいな感じで書かれることが多いので、文字よりは読み方を覚えておく方が大切です。
これらはまとめてグリークス、ギリシャ指標と呼ばれます。
グリークスは何を表しているか?
グリークスは、オプション価格(プレミアム)の感応度を表すパラメータとして使われます。
以前のオプション価格の変動要因の記事を書きました。
価格の主な変動要因としては、以下の3つが挙げられます。
- 原資産価格の変化
- ボラティリティの変化
- 残存期間の減少
それぞれに対してのパラメータとして、以下のグリークスが対応します。
- 原資産価格の変化 ➡ デルタ
- ボラティリティの変化 ➡ ベガ
- 残存期間の減少 ➡ セータ
例えば、原資産価格が変化することによりオプション価格がどのぐらい変わるのかは、デルタを確認すれば分かります。びしっと数字で出てきます。めちゃくちゃいいですよね?
グリークスを見れば現在のポジションは何が起こったときのリスクが高くなっているかを把握することができるので、ポートフォリオのリスク管理の用途でよく使われたりします。
もちろんオプションの特性を知ることは、仕掛ける際の権利行使日、権利行使価格の選択にも役立ちます。
それぞれのパラメータについて詳しく見ていく前にこれでもかと出てくる用語がありますので、おさらいをしておきます。これらの用語は以後は略語で記載します。
- アット・ザ・マネー(ATM)
本質的価値がゼロの状態(原資産価格=権利行使価格) - イン・ザ・マネー(ITM)
本質的価値がゼロより大きい状態(コールの場合、原資産価格>権利行使価格) - アウト・オブ・ザ・マネー(OTM)
本質的価値がゼロより小さい状態(コールの場合、原資産価格<権利行使価格)
よし、準備は完了です。では、いきましょう。
デルタ(Δ)
デルタは、原資産価格の変化に対するプレミアムの感応度を表す数字です。原資産価格が1ドル変動したときにプレミアムがいくら変わるのかを推測するのに使われます。
コールは0~1の範囲で、原資産価格が上がるほど1に近づき、下がるほど0に近づきます。原資産価格が権利行使価格と同じ(ATM)になるとき、おおよそ0.5となります。
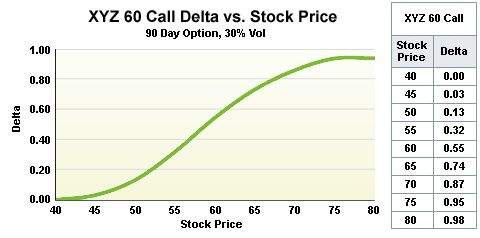
出典:OIC
プットの場合は0~-1の範囲で、原資産価格が上がるほど0に近づき、下がるほど-1に近づきます。
例えばプレミアムが2.50ドルでデルタが0.30のコールオプションがあったとすると、対象の原資産価格が1ドル上昇した際のプレミアムは
5.00 + 0.75 = 5.75
と計算することができます。
コール、プットでいくつかの例を表にしました。
プットの場合はデルタがマイナスなので、原資産価格が下落したときにデルタを引き算することでプレミアムは上昇します。コールでもプットでも原資産価格が上昇したときはデルタを足し算、下落したときはデルタを引き算です。
| 種類 | プレミアム | デルタ | プレミアム [原資産1ドル上昇後] | プレミアム [原資産1ドル下落後] |
|---|---|---|---|---|
| コール | $5.00 | +0.75 | $5.75 | $4.25 |
| コール | $2.50 | +0.30 | $2.80 | $2.20 |
| プット | $3.00 | -0.25 | $2.75 | $3.25 |
| プット | $4.00 | -0.60 | $3.40 | $4.60 |
これがデルタの使い方の基本です。ぶれはでますが、株価の変動によってどれぐらい上下するのかが数字で推測できる。素晴らしいとしか言いようがありません。
さらにデルタには別の便利な使い道もあります。
デルタは、オプションがITMで満期を迎える確率として利用できます。
もちろん精度は高くなくざっくりとした目安としてという感じですが、効果は抜群です。
例えば、プット売りをする際に感覚で権利行使価格を選んでいた人がデルタを使うとどの銘柄に対してもどんな状況下においても同じぐらいのリスクを取ったオプションを選べるようになります。それによりリスクの取りすぎ、取らなさすぎを回避できるようになります。
この確率の考え方はデルタの特性を理解するのにも役立ちます。
原資産価格がATMのコールがITMで満期を迎える確率はどれくらいかを考えると少しでも原資産価格が上がればITM、逆に少しでも下がればOTMです。つまり確率は50%と考えられます。このときのデルタは0.5です。
オプションがITMになればなるほどITMで満期を迎える確率が上がるので確率は100%に近づきます。確率が100%に近づくのに連動してデルタは1に近づいています。
基本がわかったところでデルタの特性について少し深堀りします。
デルタとインプライド・ボラティリティ
インプライド・ボラティリティの大小によってデルタの値はどうなるのかを見てみます。くどいので以後はインプライド・ボラティリティは単純にボラティリティと書きます。
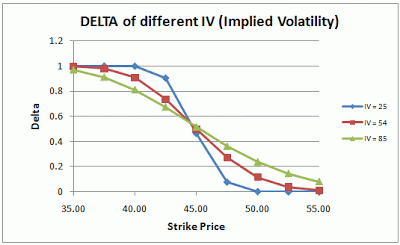
出典:Options Trading Beginner
上図は異なるボラティリティによるコールの権利行使価格とデルタの関係を示しています。プットはコールの逆で考えられるのでコールだけを見ていきます。
アット・ザ・マネー(ATM)
権利行使価格45ドルがATMです。 ATMではボラティリティに関係なくデルタは約0.5となります。ボラティリティが大きかろうが小さかろうがITMになる確率は50%と考えられます。
イン・ザ・マネー(ITM)
ボラティリティが低い方がデルタが大きくなります。
すでにITMの状態なので、現状維持ができればITMで満期を迎えられます。ボラティリティが小さいほど現状維持の確率が高いのでデルタは大きくなります。逆にボラティリティが高いとディープITM(原資産価格が権利行使価格を大きく上回る状態)でも急に原資産価格が暴落し、ITMではなくなってしまう可能性が残るのでデルタは比較的低い状態で留まります。
アウト・オブ・ザ・マネー(OTM)
ボラティリティが高い方がデルタが大きくなります。
OTMになってしまっている場合は、現状維持ではだめです。ボラティリティが高い方が原資産価格が急騰してITMになる可能性が高くなるのでデルタが大きくなります。
デルタと残存期間
残存期間の大小によってデルタの値はどうなるのかを見てみます。
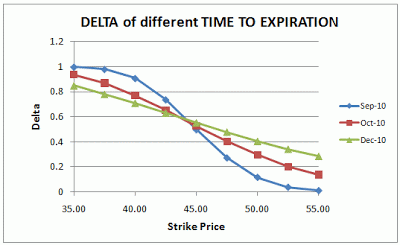
出典:Options Trading Beginner
上図は異なる残存期間による権利行使価格とデルタの関係を示しています。
アット・ザ・マネー(ATM)
権利行使価格45ドルがATMです。ATMでは残存期間に関わらずデルタはおよそ0.5となります。
イン・ザ・マネー(ITM)
残存期間が少ないほどデルタが大きくなります。
期間が長いほど原資産価格は現在と離れた価格になる可能性が高くなります。逆に残存期間が少ないほど現状維持の確率は高くなり、デルタは大きくなります。
アウト・オブ・ザ・マネー(OTM)
残存期間が多いほどデルタが大きくなります。
補足は割愛します。なんでそうなるのか?ここまで見てきた方なら分かるはずです。
ガンマ(Γ)
ガンマは、原資産価格の変化に対するデルタの感応度を表す数字です。原資産価格が1ドル変動したときにデルタがいくら変わるのかを推測するのに使われます。
デルタはATMのときに一番不安定な状態となり、変動が大きくなります。そのためガンマはATMで最大となります。
デルタはあくまでその瞬間の値なので原資産価格が変動するとデルタの値も変わります。ガンマの値を使うことによってデルタの値がいくらぐらいに変わるのかを予測ができます。
ガンマの範囲はコール、プットに関わらず0~1です。原資産価格が上昇したときはガンマを足し算、下落したときはガンマを引き算です。
| 種類 | デルタ | ガンマ | デルタ [原資産1ドル上昇後] | デルタ [原資産1ドル下落後] |
|---|---|---|---|---|
| コール | +0.50 | +0.05 | +0.55 | +0.45 |
| コール | +0.20 | +0.02 | +0.22 | +0.18 |
| プット | -0.35 | +0.03 | -0.32 | -0.38 |
| プット | -0.55 | +0.10 | -0.45 | -0.65 |
デルタは、オプションがITMで満期を迎える確率として考えた場合に、ガンマは何を表すことになるでしょうか?
ガンマは原資産価格の変動によって確率がどの程度変わるのかを表します。
ガンマが大きいと原資産価格の変動によってデルタは大きくブレることになります。デルタを確率の目安として使うときは、ガンマを確認することで将来の確率の変化に対する推測ができるようになります。
ガンマとインプライド・ボラティリティ/残存期間
ガンマはボラティリティの影響と残存期間の影響が似ているので一気に説明します。
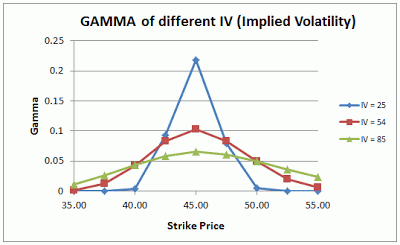
出典:Options Trading Beginner
出典:Options Trading Beginner
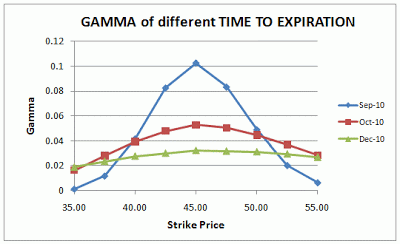
上図は異なるボラティリティによる権利行使価格とガンマの関係、異なる残存期間による権利行使価格とガンマの関係を示しています。
ATMは権利行使価格45ドルです。どのボラティリティ、残存期間でもATMにおいてガンマが最大値を取っています。
ボラティリティ小 残存期間短
ボラティリティが小さい場合、残存期間が短い場合は、デルタはATM近辺では大きく動いていました。逆にITM、OTMではデルタの動きは小さいです。
このようなデルタの特性をガンマから捉えると、ガンマは権利行使価格によって値が大きく変動し、高い山の形となります。
ボラティリティ大 残存期間長
ボラティリティが大きい場合、残存期間が長い場合は、デルタはATMを境に大きく変動することはありません。また、ITMやOTMの状態においてもデルタは極端な値とはなっておらず、原資産価格と共に変動をします。
このようなデルタの特性をガンマから捉えると、ガンマは権利行使価格によって変化の少ないなだらかな山の形となります。
ベガ(ν)
ベガは、インプライド・ボラティリティの変化に対するプレミアムの感応度を表す数字です。インプライド・ボラティリティが1%変動したときにプレミアムがいくら変わるのかを推測するのに使われます。
権利行使価格、満期日が同じであれば、プット、コールとも同一の値となり、ATM付近で最大となります。
インプライド・ボラティリティの上昇はプレミアムの上昇にのみ寄与するのでベガは常に正の値になります。
ベガとインプライド・ボラティリティ
出典:The Options Guide
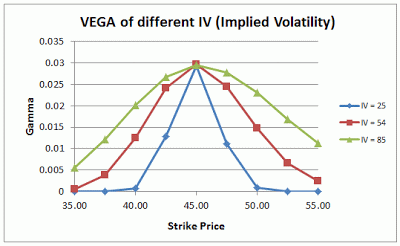
上図は異なるボラティリティによる権利行使価格とベガの関係を示しています。
ATMは権利行使価格45ドルです。どのボラティリティでもATMにおいてベガが最大値を取っています。
ボラティリティ大 ボラティリティ小
ボラティリティが大きい方が値幅が出てくる可能性が高いので、 ITMやOTMの状態においてもベガが大きくなります。そのため、ボラティリティが大きいほど権利行使価格によって変化の少ないなだらかな山の形となります。
逆にボラティリティが小さいとATMから離れると急激にベガが小さくなります。 そのため、 ベガは権利行使価格によって値が大きく変動し、高い山の形となります。
ボラティリティに関わらずATMの値がほぼ同じ値を取っているのはベガだけに見られる特徴です。
ベガと残存期間
出典:The Options Guide
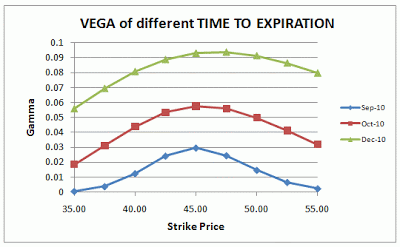
上図は異なる残存期間による権利行使価格とベガの関係を示しています。
ATMは権利行使価格45ドルです。どの残存期間でもATMにおいてベガが最大値を取っています。
残存期間短 残存期間長
満期までの日数が長いオプションの方がボラティリティの影響を強く受けるため、ベガの値は大きくなります。
どの権利行使価格の時点においても残存期間が長いオプションの方がベガが大きくなるので、グラフは残存期間が長くなるほど上に移動するイメージとなります。
セータ(θ)
セータは、時間経過(タイムディケイ)に対するプレミアムの感応度を表す数字です。1日経過(休日含む)するごとにプレミアムがいくら失われるのか推測するのに使われます。
時間的価値はATMにおいて最大となりますので、セータの値もATMで最大となります。また、満期においては時間的価値もセータもゼロとなります。
時間経過はプレミアムの下落にのみ寄与するのでセータは常に負の値になります。
セータとインプライド・ボラティリティ
出典:Options Trading Beginner
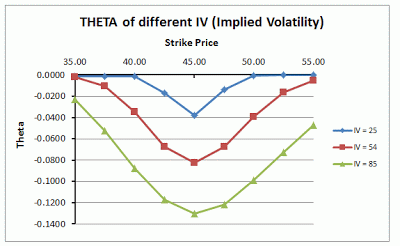
上図は異なるボラティリティによる権利行使価格とセータの関係を示しています。
ATMは権利行使価格45ドルです。どのボラティリティでもATMにおいてセータが最大値を取っています。
ボラティリティ大 ボラティリティ小
残存期間が一定の場合、ボラティリティが大きいほど値幅が出てくる可能性が高く、時間的価値が高くなります。そのため、原資産価格と権利行使価格の位置に関係なくボラティリティが大きいほうがセータが大きくなります。
セータと残存期間
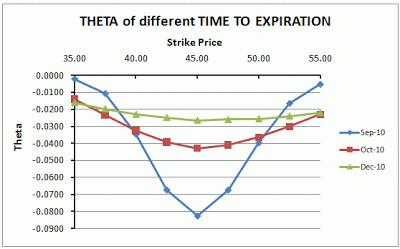
出典:Options Trading Beginner
上図は異なる残存期間による権利行使価格とセータの関係を示しています。
ATMは権利行使価格45ドルです。どの残存期間でもATMにおいてセータが最大値を取っています。
残存期間短 残存期間長
残存期間が短くなれば、もちろん時間的価値は少なくなります。しかし、シータが表しているのは1日の時間経過によって失われるプレミアムです。ATM付近にある場合は、残存期間が短いほどシータは大きくなります。これは、残存期間が短いITM、OTMのオプションはほとんど時間的価値がなくなっていることを考えるとすんなりと理解できると思います。
残存期間が長いオプションは時間的価値が毎日コツコツと削られていくイメージです。ATMから離れるほどシータは小さくなりますが、影響は軽微です。
キャッシュ・セキュアード・プットは、OTMのプットを売ってプレミアムを得るのが定石です。株価が動かなくても時間の経過とともにタイムディケイの効果で毎日セータ分だけのプレミアム減少が期待できます。
先ほど見たように残存期間が長い場合は、ATMとITM/OTMでセータの値は大きく変わりません。そして、権利行使日が近づくにつれてATMはセータが増加し、ITM/OTMではセータが減少します。この傾向は権利行使日まで30日を過ぎてくると大きくなってきます。
下図は9/3時点でのセータの値を示しています。権利行使2010年10月(残存期間38日)と2010年12月(残存期間101日)ではセータの差は小さいですが、2010年9月(残存期間10日)と2010年10月はセータの差が大きくなっています。
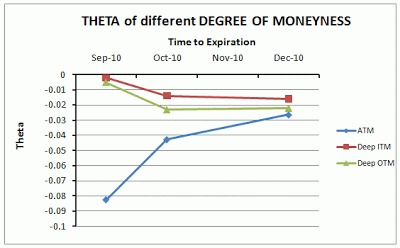
出典:Options Trading Beginner
セータが小さい=タイムディケイの効果が小さくなっているということなので、満期前にプットを買い戻して新たなキャッシュ・セキュアード・プットを仕掛けるのもよいかもしれません。
まとめ
記事が長くなったので最後にまとめてもう一度書いておきます。
グリークス=オプション価格の感応度を表すパラメータ
主なものは以下の4つ
- デルタ:原資産価格1ドルの変動に対するオプション価格の感応度
- ガンマ:原資産価格1ドルの変動に対するデルタの感応度
- シータ:時間経過1日に対するオプション価格の感応度
- ベガ:ボラティリティ1%の変化に対するオプション価格の感応度
グリークスを確認することによって、現在自分が持っているポジションがどのようなリスクやチャンスがあるのかを感覚ではなく、数字で掴むことができます。
あとがき
現在私がメインで行っているオプション取引はキャッシュ・セキュアード・プットですが、コツコツドカンでなかなか利益を出せていません。
オプション取引は、ポジションを取った後のメンテナンス(どこで利確するか、損切りするか)の方が大切な気がしてきています。
そこで役立ちそうなのが、今回の勉強したオプショングリークスです。メンテナンスは不得意分野ですが、稼げるオプショントレーダーになるために精進します!
最後に1つ。今回記事を書いていて一番びっくりしたのはめちゃくちゃそれっぽい顔してグリークスの一員となっているベガ(ν)が、ギリシャ文字ではないってことです。うーむ、モヤモヤしますね。





コメント