オプショントレーダーたる者、オプション価格(プレミアム)がどのような要因によって変動するのかを抑えておかねばなりません。
色々ややこしい話があるのですが、この記事ではややこしい話はなしにしてプレミアムの変動要因についてなるべく簡単に紹介します。
本質的価値と時間的価値
オプションとは、将来の決められた期日(満期日)にあらかじめ決められた価格(権利行使価格)で原資産を買う権利(コール)、または売る権利(プット)のことでした。
その権利が持っている価値は、なんなのか?そこには「本質的価値」と「時間的価値」という2種類の価値があります。
数式で表すと
プレミアム = 本質的価値 + 時間的価値
となります。
本質的価値とは、オプションの権利行使をしたときに得られる利益に対してついている価値です。
時間的価値とは、満期日までに本質的価値が増加することへの期待に対してついている価値です。
それぞれの価値について詳しく見てみます。
本質的価値
本質的価値はオプションの権利行使をしたときに得られる利益に対してついている価値ですので、原資産価格が権利行使価格より高い状態のときのみに発生する価値です。
オプションは原資産価格に対する権利行使価格の位置によって「イン・ザ・マネー(ITM)」「アット・ザ・マネー(ATM)」「アウト・オブ・ザ・マネー(OTM)」の3つに分類することができます。
コールとプットでは関係性が逆になります。
| 分類 | コール | プット |
|---|---|---|
| イン・ザ・マネー | 原資産価格 > 権利行使価格 | 原資産価格 < 権利行使価格 |
| アット・ザ・マネー | 原資産価格 = 権利行使価格 | 原資産価格 = 権利行使価格 |
| アウト・オブ・ザ・マネー | 原資産価格 < 権利行使価格 | 原資産価格 > 権利行使価格 |
本質的価値はオプションがイン・ザ・マネーの状態にあるときのみに発生し、以下の計算式で表すことができます。
コールの本質的価値 = 原資産価格 – 権利行使価格
プットの本質的価値 = 権利行使価格 – 原資産価格
オプションがアット・ザ・マネー、アウト・オブ・ザ・マネーの状態にあるときは本質的価値はゼロとなるため、以下の式が成り立ちます。
プレミアム = 時間的価値
これは本質的な価値など何もなく、夢のみが詰め込まれた状態です。
時間的価値
時間的価値とは、将来の原資産の価格変動によって本質的価値が増加することへの期待に対してついている価値です。時間的価値は基本的に時間経過とともに価値が下がっていきます。そして、満期時点ではゼロになります。
オプションという商品の特徴は、権利を行使する日が決められている点です。よって時間的価値こそがオプションをオプションたらしめているものと言うことができます。
時間的価値は本質的価値のように単純に決まるものではなく以下のような複数の要因によって価値がつけられています。
- 満期までの残存日数
- インプライド・ボラティリティ
- 配当
- 安全利子率(無リスク金利)
複数の要因がありますが、主な要因だけに焦点を当てると「満期までの残存日数」と「インプライド・ボラティリティ」の2つだけに絞ることができます。
満期までの残存日数
満期までの残存日数が長いほど、原資産価格が現在値から大きく動く可能性は高くなります。
例えば、A社の株が1日で10%上がったり、下がったりする可能性はほとんどないですが、1か月後に10%上がっていたり、10%下がっていたりすることはまあまああります。
原資産価格の変動により、原資産価値が増加する可能性が高くなるのでその期待に対する価値も高くなります。
インプライド・ボラティリティ
ボラティリティは、変動率を表します。数値が大きいほど、価格変動が大きいことを示しています。
ボラティリティには「ヒストリカル・ボラティリティ」と「インプライド・ボラティリティ」の2種類があります。
ヒストリカル・ボラティリティ:過去の値動きを元に算出した将来の変動率
インプライド・ボラティリティ:市場参加者の期待や予測などから形成される将来の変動率
過去の値動きやアナリストの目標株価、景気の動向、夢、希望、不安、誤発注、その他もろもろが反映されて形成されたものが、インプライド・ボラティリティになります。このインプライド・ボラティリティが時間的価値へ大きな影響を与えます。
市場参加者の考える将来の変動率(インプライド・ボラティリティ)が大きくなるほど、原資産価格が現在値から大きく動くと予想する人が多くなります。
その結果、高いプレミアムを払ってでもオプションを買いたい人が増え、オプションのプレミアムは高くなります。
数字として表現されるインプライド・ボラティリティはこのプレミアムから算出されます。
ブラックショールズモデルなどのオプションの理論価格計算式に実際に取引されているオプション価格を適用することで、ボラティリティを逆算できます。
市場参加者の思惑を反映した結果として価格が形成されているオプション価格から導き出したその数値こそがインプライド・ボラティリティなのです。
なんだか狐につままれたような感じですが、そういうことなのです。
さて、このインプライド・ボラティリティが大きくなるのはどんなときでしょう。
決算前や大統領選挙などの大きく原資産価格に影響を与えるイベントの前は、イベント通過前後の価格変動が大きくなる可能性が非常に高いのでインプライド・ボラティリティも大きくなります。これらのイベントの前はたとえ満期までの残存日数が少なかったとしても時間的価値の減少は比較的小さくなります。
原資産価格の変動もインプライド・ボラティリティの価格を動かす要因になります。基本的に原資産価格が上がるとインプライド・ボラティリティは下がり、原資産価格が下がるとインプライド・ボラティリティは上がる性質を持っています。
恐怖指数という呼び名でも有名なVIX指数は、S&P500のオプション価格を用いて算出されたインプライド・ボラティリティの数値です。以下のチャートを見ると原資産価格とインプライド・ボラティリティの動きが逆行する性質があることが良く分かります。
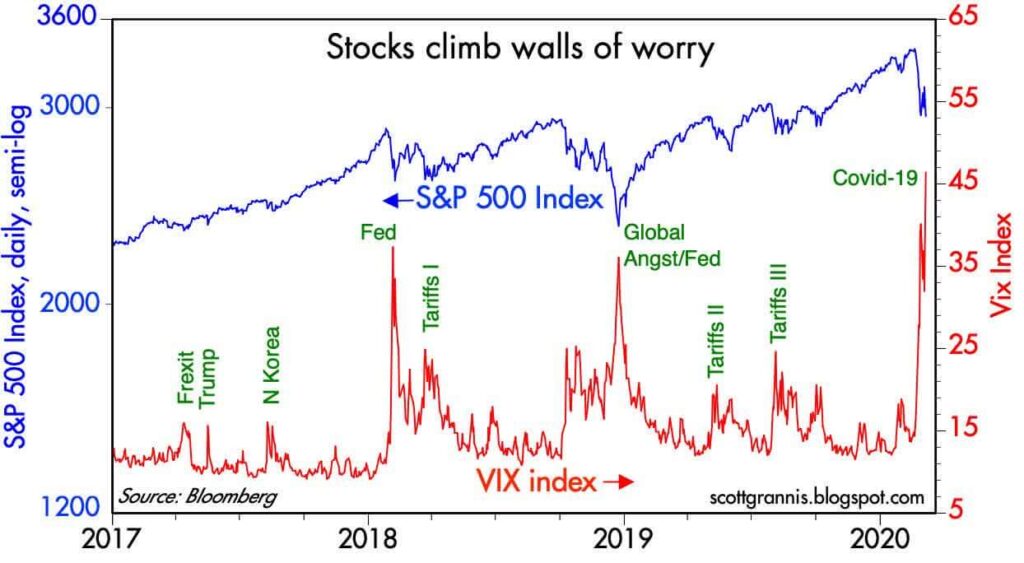
出典:Seeking Alpha
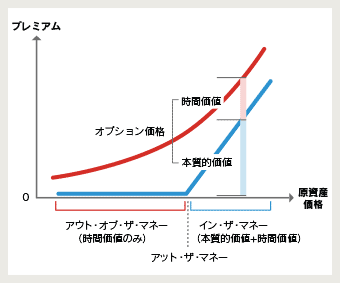
本質的価値と時間的価値の関係図
本質的価値と時間的価値の関係図を使ってそれぞれの価値の付き方についておさらいをします。
図は満期前のコールオプションのプレミアムと原資産価格の関係を示しています。
出典:IG証券
A社の権利行使価格100円のコールオプションを持っているとして、原資産価格の状況によりどのようにプレミアムがついているのかを見てみます。
① 原資産価格が110円の場合、プレミアムは20円
- 原資産価格 > 権利行使価格なので、オプションはイン・ザ・マネー
- 本質的価値 = 原資産価格 – 権利行使価格 = 110 – 100 = 10円
- 時間的価値 = プレミアム – 本質的価値 = 20 – 10 = 10円
② 原資産価格が100円の場合、プレミアムは15円
- 原資産価格 = 権利行使価格なので、オプションはアット・ザ・マネー
- 本質的価値 = 0円
- 時間的価値 = プレミアム = 15円
③ 原資産価格が90円の場合、プレミアムは10円
- 原資産価格 < 権利行使価格なので、オプションはアウト・オブ・ザ・マネー
- 本質的価値 = 0円
- 時間的価値 = プレミアム = 10円
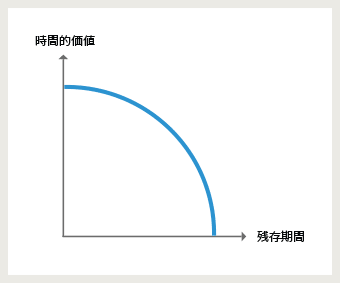
時間的価値は、満期までの残存日数と共に落ちていきます。満期では時間的価値がゼロとなり、本質的価値のみとなります。
出典:IG証券
プット売りをしてプレミアムを受け取る戦略は、一般的には現在価格より権利行使価格が安い(アウト・オブ・ザ・マネー)のオプションを選びます。
上で見てきたようにアウト・オブ・ザ・マネーのオプションは時間的価値しかありません。株価が下がってくるにつれ、プットオプションは権利行使ができる可能性が高くなってきます。それに伴って時間的価値が大きくなります。
そして、権利行使価格を下回ると時間的価値に加えて本質的価値もプレミアムに上乗せされます。本質的価値の上昇は株価の下落と負の比例関係なので、株価が下がるほどプレミアムは急激に上昇していきます。
これがキャッシュ・セキュアード・プットをして含み損が急増するメカニズムです。想定外に株価が下落したときなどには注意が必要です。
あとがき
最後までお読みいただきありがとうございます。ざっくりと言いながら説明が長いじゃねぇか!という声が聞こえてきそうですが、これでも頑張ったつもりです。
自分の中では理解している内容と思っているのですが、それを文字に起こして伝えるというのは至難の業ですね。時間ばっかりかかりますが、いいアウトプットがなかなか出てきません。少しでも理解の役に立てることができれば幸いです。
これからもブロガーとして精進します。。
本記事を書くにあたって以下の記事を参考にさせていただきました。







コメント